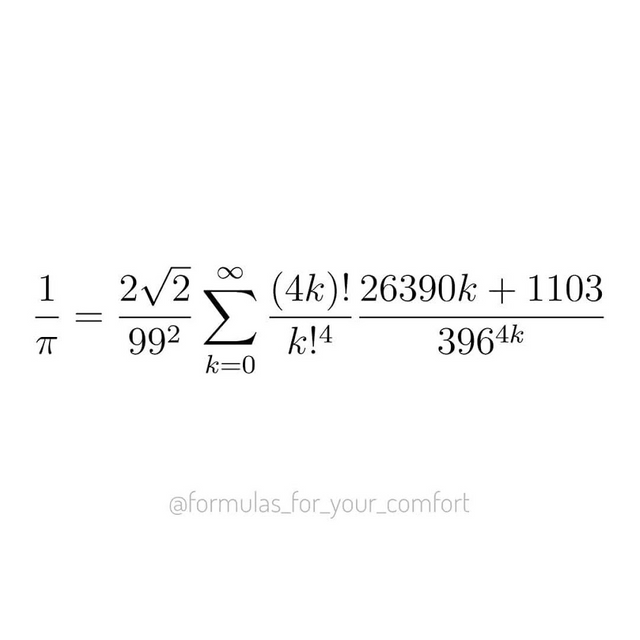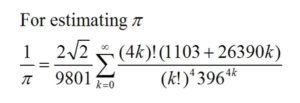0027: Part 6, Ramanujan's pi formulas and the hypergeometric function - A Collection of Algebraic Identities
Cliff Pickover on Twitter: "Mathematics. A formula from Indian mathematician Ramanujan. Golden Ratio, e, and Pi dance in delight. https://t.co/PWnPd0a3aW" / Twitter
National Mathematics Day 20212: 9 Interesting Facts about Genius Mathematician Srinivasa Ramanujan
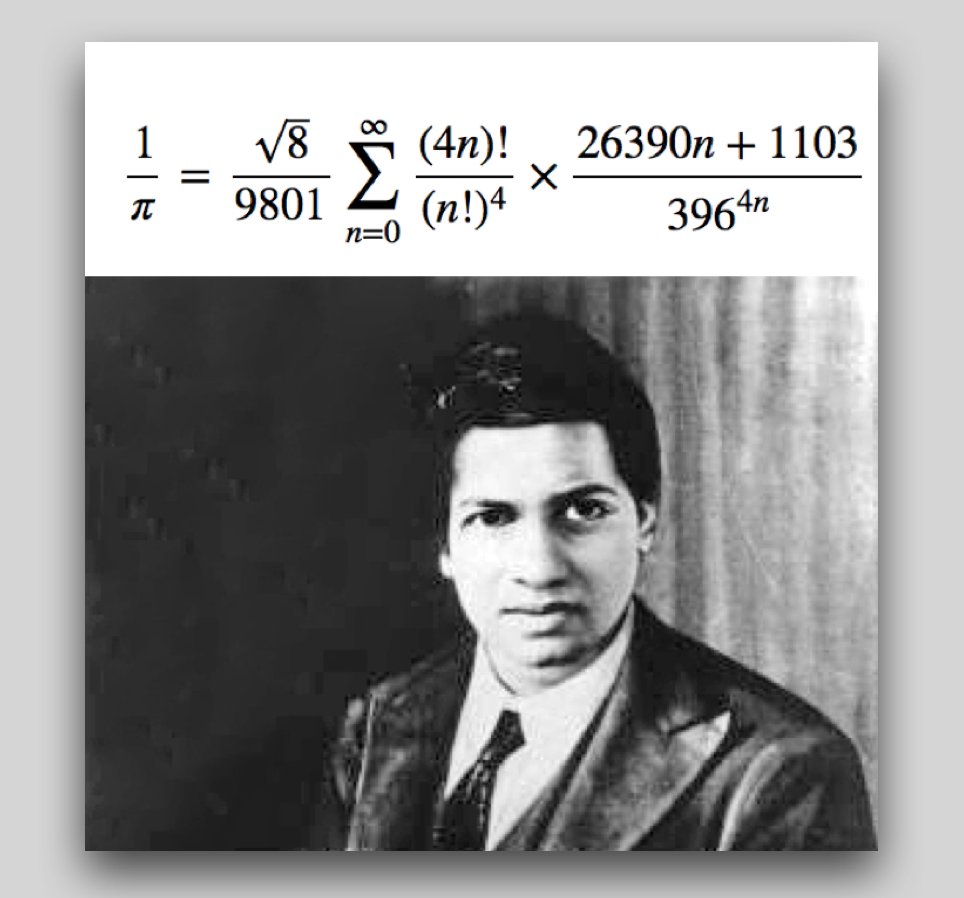
wink on Twitter: "Remembering Srinivasa Ramanujan's formula to compute the value of #Pi and wishing everyone a Happy #PiDay! https://t.co/FK3fhQOyxC" / Twitter
GitHub - nqureshi/ramanujan-pi-approximation
Ramanujan's Pi Formulae, 1914 :: Chudnovsky Brothers' Pi Formula , 1988 - YouTube
A monstrous formula : Ramanujan's approximation of pi — Steemit
0019: Article 9 (More Pi Formulas) - A Collection of Algebraic Identities
Ramanujan-like formulae for $$\pi $$ π and $$1/\pi $$ 1 / π via Gould–Hsu inverse series relations | SpringerLink
Solved Ramanujan's Formula for Pi First found by Ramanujan. | Chegg.com
Pi Formulas -- from Wolfram MathWorld
Ramanujan's Formula for Pi First found by Ramanujan. | Chegg.com
Pi Table with Ramanujans,Chudnovsky Formulas
Convergent hypergeometric Ramanujan-like series for 1/π 2 | Download Table
Estimating pi
Ramanujan's Magnificent Formula for Pi: 9801/(1103√8)=π | by Sunny Labh | Cantor's Paradise
Ramanujan pi formula | Learnodo Newtonic
what is pi in Maths||π||A brief history of pi in India|Ramanujan's pi formula||Latest records of Pi. - YouTube
Solved Ramanujan's sum of 1/pi The goal of this project is | Chegg.com
Although he died at the age of 32, Ramanujan left behind a large number of mathematical results, a… | Physics and mathematics, Mathematics education, Math tutorials
Who Was Ramanujan?—Stephen Wolfram Writings
Extra-math - 📊Ramanujan Pi-Formula & Derivation | Facebook
How accurate is Ramanujan's PI series? - Quora
Ramanujan's sum - Wikipedia
